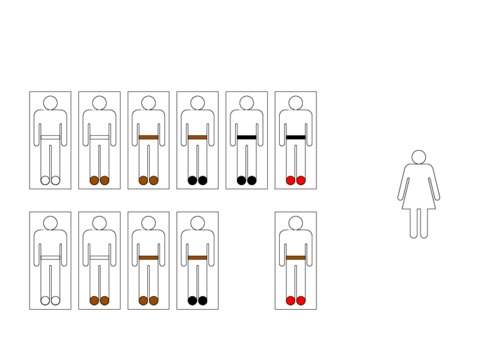
Bx Examples Repository
Title: BeltAndShoes
Version: 0.1
Type: Precise
Overview
An accessible illustration of a BX that is not undoable/history-ignorant/very-well-behaved.
My wife saves me from making a faux pas by breaking the Laws of Fashion, in particular that thou shalt not wear a brown belt with black shoes, or a black belt with brown shoes. Before I leave the house, she corrects any inconsistencies in my outfit. One morning, I put on a brown belt and brown shoes; then I decide that the brown shoes are too scruffy for today's meetings, so I change to black shoes; then my wife notices, and changes my belt to black to match; finally, I decide that the shoes are not comfortable enough for the walk to work, so I change into my red trainers; my wife doesn't care what belt I wear with red trainers, so I leave for work with black belt and red trainers. The next morning, a similar story unfolds, except that my wife does not notice me with black shoes and brown belt, so doesn't change my belt; again I change into my red trainers; now my wife checks my outfit, doesn't care what belt I wear with red trainers, and I leave for work with brown belt and red trainers.
Models
$\mathit{Shoes} = \{ \mathit{none}, \mathit{brown}, \mathit{black}, \mathit{red} \}$
$\mathit{Belt} = \{ \mathit{none}, \mathit{brown}, \mathit{black} \}$
Consistency
Brown and black should not be worn together; anything else is fine.
$R(s,b) \equiv (s = \mathit{brown} \Rightarrow b \ne \mathit{black}) \land (s = \mathit{black} \Rightarrow b \ne \mathit{brown})$
Consistency Restoration
There is some freedom when fixing a fashion faux pas of brown belt with black shoes or black belt with brown shoes; here, we make sure the shoes are the same colour as the belt.
$\begin{array}{lcl} \overrightarrow{R}(\mathit{brown},\mathit{black}) &=& \mathit{brown} \\ \overrightarrow{R}(\mathit{brown},b) &=& b \quad\mbox{when $b \ne \mathit{black}$} \\ \overrightarrow{R}(\mathit{black},\mathit{brown}) &=& \mathit{black} \\ \overrightarrow{R}(\mathit{black},b) &=& b \quad\mbox{when $b \ne \mathit{brown}$} \\ \overrightarrow{R}(s,b) &=& s \quad\mbox{when $s \notin \{\mathit{brown},\mathit{black}\}$} \end{array}$
Backwards consistency restoration $\overleftarrow{R}$ is not relevant for this illustration, but could be defined similarly to forwards.
Properties
- correct (shoes and belt are consistent afterwards)
- hippocratic (when shoes and belt are consistent, no change is made)
- neither undoable or history ignorant (let $s = \mathit{black}, s' = \mathit{red}, b = \mathit{brown}, b' = \mathit{black}$; then $\overrightarrow{R}(s',\overrightarrow{R}(s,b)) = b'$ but $\overrightarrow{R}(s',b) = b$)
Variants
Mike Johnson observes that it is arguable that this illustration does not break PutPut, provided you think of it from an ordered perspective — that is, it satisfies Monotonic PutPut. Specifically, the belt states are ordered with $\mathit{none} < \mathit{brown}$ and $\mathit{none} < \mathit{black}$, and similarly the shoe states are ordered with $\mathit{none}$ below any colour of shoes. Then the only monotonic sequences of changes to my shoes are trivial — all but one of them must be the identity — and so putting a composition of steps coincides with putting each of them in turn.
Discussion
This example was used in the introductory lecture at the Summer School on BX and Shonan Meeting Seminar 091 on BX.
References
Author(s)
Jeremy Gibbons and Sue Gibbons
Reviewer(s)
Comments
Artefacts